格拉姆-施密特正交化概述
在数学的奇妙世界中,正交化是一个非常重要的过程,尤其是在向量空间和线性代数的领域。格拉姆-施密特正交化方法不仅可以帮助我们理解向量之间的关系,还能将一个线性无关的向量组转化为正交的向量组。这一过程在许多应用中都有着广泛的用途,包括信号处理、数据分析以及计算机图形学等。接下来,我们将深入探讨这一方法的步骤、原理及其应用技巧,带你领略正交化的魅力。
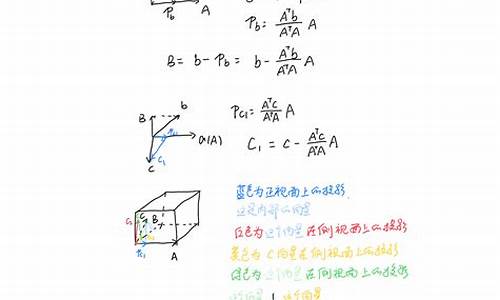
正交化的基础知识
在深入格拉姆-施密特正交化之前,我们需要了解什么是正交和正交化。简单来说,两个向量如果相互垂直,则称为正交。在多维空间中,正交向量组是线性独立的,这意味着它们不会“重叠”或“相互干扰”。正交化的目的是通过一系列操作,使得原有向量组中的每个向量都与其他向量正交。
正交的定义
正交是指两个向量的点积为零。换句话说,如果有两个向量 A 和 B,那么它们正交的条件可以用以下公式表示:
A·B = 0
正交化的必要性
正交化的过程在许多数学和工程问题中是至关重要的。例如,在最小二乘法中,正交向量有助于简化计算,提高数值稳定性。
格拉姆-施密特正交化的步骤
了解格拉姆-施密特正交化的步骤,可以让我们更好地掌握这一技术。通常,这一过程包括以下几个步骤:
选择向量
首先,从给定的线性无关向量组中选择第一个向量,记作 v1。这个向量将被用作新的正交基的第一个向量,记作 u1。
构造正交向量
接下来,对于第二个向量 v2,我们需要从中减去在 u1 上的投影。具体步骤如下:
u2 = v2 - proj_u1(v2)
其中 proj_u1(v2) 表示 v2 在 u1 上的投影。
重复步骤
继续对后续的向量进行同样的操作,直到处理完所有的向量。对于第三个向量 v3,计算方式为:
u3 = v3 - proj_u1(v3) - proj_u2(v3)
格拉姆-施密特正交化的实例
为了更好地理解这一过程,下面是一个简单的示例。假设我们有三个二维向量:
v1 = (1, 1)
v2 = (1, 0)
v3 = (0, 1)
通过应用格拉姆-施密特正交化,我们可以逐步得到正交向量组 u1, u2 和 u3。
实例计算
1. 选择 v1 作为 u1:
u1 = v1 = (1, 1)
2. 计算 u2:
proj_u1(v2) = (v2·u1)/(u1·u1) u1 = (1·(1, 1))/(2) (1, 1) = (0.5, 0.5)
u2 = v2 - proj_u1(v2) = (1, 0) - (0.5, 0.5) = (0.5, -0.5)
3. 计算 u3:
proj_u1(v3) = (v3·u1)/(u1·u1) u1 = (0·(1, 1))/(2) (1, 1) = (0, 0)
proj_u2(v3) = (v3·u2)/(u2·u2) u2 = ((0, 1)·(0.5, -0.5))/(0.5) (0.5, -0.5) = (0, 0)
u3 = v3 - proj_u1(v3) - proj_u2(v3) = (0, 1) - (0, 0) = (0, 1)
最终我们得到了正交向量组 u1, u2 和 u3。
格拉姆-施密特正交化的应用
这一方法在众多领域中都有实际应用,以下是一些典型的例子:
信号处理
在信号处理领域,正交化可以用于信号的解调与滤波,帮助提取所需信息,同时减少噪声干扰。
计算机图形学
在计算机图形学中,正交向量常用于模型变换,确保物体的旋转、缩放和定位不受影响。
数据分析与机器学习
在数据降维和特征选择中,正交基可以提高算法的效率,使得模型更具鲁棒性。
总结归纳
格拉姆-施密特正交化方法是理解线性代数和向量空间的重要工具。它不仅提供了将线性无关向量组转换为正交向量组的有效方法,而且在多个应用领域中具有显著意义。掌握这一过程后,你将能够更加自如地处理各种数学和工程问题。希望这篇文章能帮助你在数学的旅程中,找到更多的乐趣和启发!
