概述
同调理论是代数拓扑中的一颗璀璨明珠,它不仅为我们提供了研究空间的工具,还揭示了许多深刻的数学原理。在本文中,我们将深入探讨同调理论的基本概念、主要应用及其在代数拓扑中的重要性。准备好迎接这场数学之旅了吗?
同调理论的基本概念
同调群的定义
同调群是一种用于描述拓扑空间性质的代数结构。简单来说,同调群能够捕捉并分类空间中的“洞”的信息。对于每个维度,存在一个对应的同调群,分别表示零维(连接成分)、一维(环)和二维(洞)等不同类型的特征。
链复形与边界算子
链复形是构建同调群的基础。它由一系列链(即简单形)组成,每个链与其边界相关联。边界算子则用于描述一个链的“边”如何构成下一个更低维度的链。通过反复应用边界算子,我们可以逐步探讨空间的复杂性。
同调理论的主要应用
在代数拓扑中的作用
同调理论最显著的应用是在代数拓扑中,它帮助我们理解不同空间之间的关系。例如,通过计算同调群,我们可以判断两个空间是否同伦等价,从而揭示它们的拓扑性质。
在几何中的应用
在几何学中,同调理论常用于研究流形的性质。通过同调群的计算,我们能够分析流形的全局性质,如曲率和拓扑类型。这些信息对物理学中的弦理论和广义相对论至关重要。
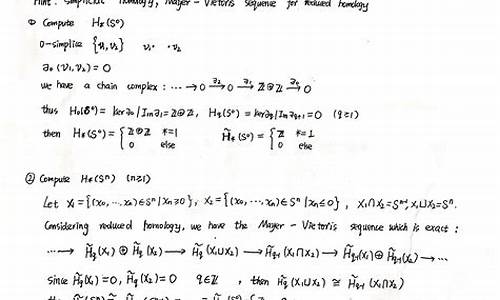
同调理论的重要性
揭示空间的本质
同调理论不仅仅是一种工具,更是一种思维方式。它教会我们用代数语言来描述空间的几何特征,进而揭示其内在的本质。这种视角的转变,常常能带来意想不到的结果。
促进数学领域的交叉
同调理论的影响远不止于代数拓扑。它与代数几何、数论、甚至物理学都有着深厚的联系。通过这种跨学科的交流,许多重要的数学定理得以形成,推动了整个数学界的发展。
结论
同调理论在代数拓扑中扮演着不可或缺的角色,它不仅提供了一种理解空间的新方式,还促进了数学各领域的交叉与融合。通过深入研究同调理论,我们不仅可以掌握空间的性质,还能开拓思维,激发更多的创新灵感。希望本文能让你对同调理论有更深的理解,继续探索这个充满魅力的数学领域吧!
