参数化几何数学百科:探索参数化曲线的性质和应用技巧
在数学的神奇世界里,参数化几何是一扇通往更深层次理解的窗户。无论你是学生、教师还是业余数学爱好者,参数化曲线的探讨都能为你打开一扇全新的大门。本文将探讨参数化曲线的基本概念、性质、应用以及如何利用这些知识解决实际问题。准备好迎接这场数学之旅了吗?
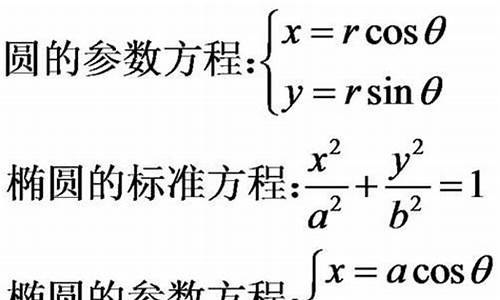
什么是参数化曲线?
定义与基本概念
参数化曲线是通过一个或多个参数来表示的曲线。与传统的隐式或显式方程不同,参数化形式允许我们用一个变量(通常是时间 t)来描述曲线上的点。例如,以二维空间中的曲线为例,我们可以用 x(t) 和 y(t) 来表示点的坐标。
参数化的优势
参数化曲线的最大优势在于其灵活性。我们可以轻松描述复杂的曲线,比如螺旋线或椭圆,而不需要解决复杂的方程。此外,参数化形式使得计算曲线的切线、法线等几何特征变得更加直观。
参数化曲线的性质
连续性与可微性
大多数情况下,参数化曲线的性质与其参数函数的连续性和可微性密切相关。若 x(t) 和 y(t) 在某个区间内均可导,则我们可以得出曲线的切线方向,这对分析曲线的形状至关重要。
弧长与曲率
弧长是测量曲线长度的重要指标,而曲率则反映了曲线的“弯曲程度”。通过参数化,可以方便地计算出弧长公式:L = ∫√(dx/dt)² + (dy/dt)² dt,而曲率 K 则可以通过公式 K = |d²y/dx²| / (1 + (dy/dx)²)^(3/2) 来找到。
参数化曲线的应用
物理中的应用
在物理学中,参数化曲线常用于描述物体运动。例如,一个小球从高处自由落下,其位置可以用时间 t 的函数表示。这种描述方式使得我们能够更容易地分析物体的速度和加速度。
计算机图形学中的应用
在计算机图形学中,参数化曲线广泛应用于动画和建模。设计师可以利用 Bézier 曲线和 B-spline 曲线进行平滑过渡和形状创建,使得生成的图像更加自然流畅。
如何有效使用参数化曲线
选择合适的参数
在进行参数化时,选择合适的参数是关键。例如,有时选择角度作为参数会比选择直线距离更有效,尤其是在处理圆形或周期性曲线时。
结合数值方法
对于复杂曲线,结合数值方法可以提高计算效率。比如,使用数值积分来估算弧长,或者利用数值微分来获取切线和法线方向。
总结与展望
参数化几何不仅是数学的一部分,更是现实世界中不可或缺的工具。通过对参数化曲线的深入理解和应用,我们不仅能更好地解决复杂问题,还能提升我们的数学思维能力。希望本文能激发你对参数化几何的兴趣,鼓励你在这条迷人的数学道路上继续前行。无论你是初学者还是资深专家,永远保持好奇心,你会在参数化的世界中发现更多的惊喜!
